Minimum no. of meeting rooms

Given an array of meeting time intervals consisting of start and end times [[s1,e1],[s2,e2],...] find the minimum number of conference rooms required.

When a room is taken, the room can not be used for anther meeting until the current meeting is over. As soon as the current meeting is finished, the room can be used for another meeting. We can sort the meetings by start timestamps and sequentially assign each meeting to a room. Each time when we assign a room for a meeting, we check if any meeting is finished so that the room can be reused. In order to efficiently track the earliest ending meeting, we can use a min heap. Whenever an old meeting ends before a new meeting starts, we reuse the room (i.e., do not add more room). Otherwise, we need an extra room (i.e., add a room).

The time complexity is O(N*log(N)).

public int minMeetingRooms(int[][] intervals) { Arrays.sort(intervals, Comparator.comparing((int[] itv) -> itv[0]));   PriorityQueue<Integer> heap = new PriorityQueue<>(); int count = 0; for (int[] itv : intervals) { if (heap.isEmpty()) { count++; heap.offer(itv[1]); } else { if (itv[0] >= heap.peek()) { heap.poll(); } else { count++; }   heap.offer(itv[1]); } }   return count; }

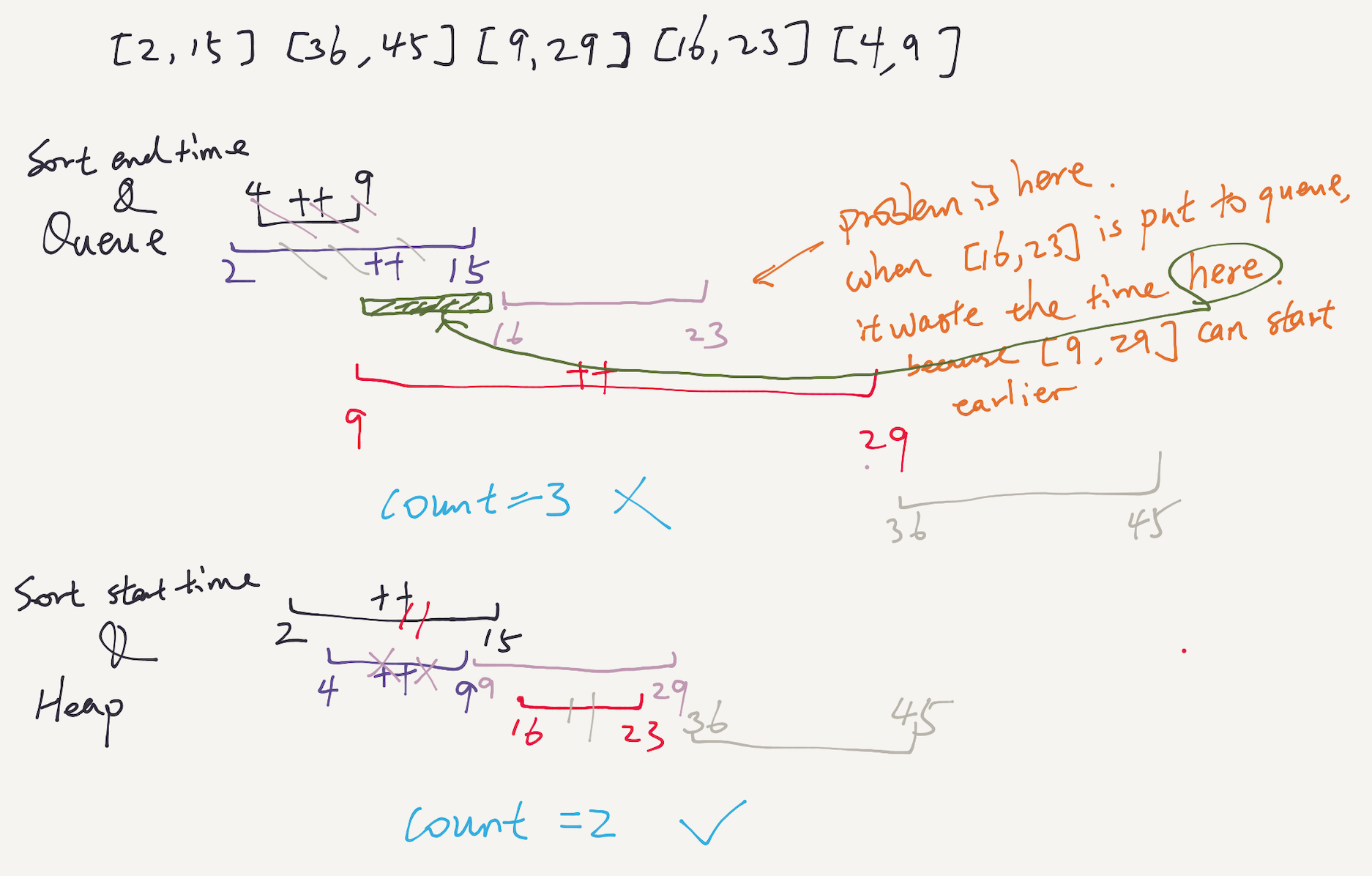
There was a discussion in the comments about why a regular queue is not good enough. I draw an example below to show why sorting based on start time and using a priority queue is necessary.