Path Sum II

Given the root of a binary tree and an integer targetSum, return all root-to-leaf paths where each path's sum equals targetSum.

A leaf is a node with no children.

 

Example 1:

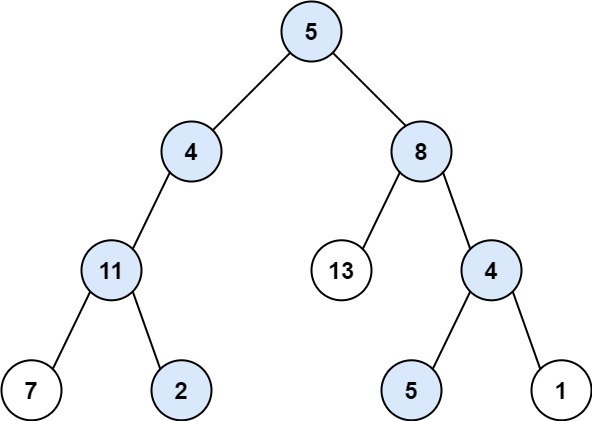
Input: root = [5,4,8,11,null,13,4,7,2,null,null,5,1], targetSum = 22
Output: [[5,4,11,2],[5,8,4,5]]

Example 2:

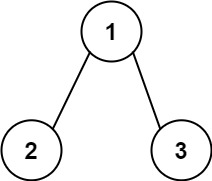
Input: root = [1,2,3], targetSum = 5
Output: []

Example 3:

Input: root = [1,2], targetSum = 0
Output: []

Solution
Approach: Depth First Traversal | Recursion
Intuition
The intuition for this approach is pretty straightforward. The problem statement asks us to find all root to leaf paths in a given binary tree. If you simply consider the depth first traversal on a tree, all it does is traverse once branch after another. All we need to do here is to simply execute the depth first traversal and maintain two things along the way:
A running sum of all the nodes traversed till that point in recursion and
A list of all those nodes
If ever the sum becomes equal to the required sum, and the node where this happens is a leaf node, we can simply add the list of nodes to our final solution. We keep on doing this for every branch of the tree and we will get all the root to leaf paths in this manner that add up to a certain value. Basically, these paths are branches and hence the depth first traversal makes the most sense here. We can also use the breadth first approach for solving this problem. However, that would be super heavy on memory and is not a recommended approach for this very problem. We will look into more details towards the end.
Algorithm
We'll define a function called recurseTree which will take the following parameters
node which represents the current node we are on during recursion
remainingSum which represents the remaining sum that we need to find going down the tree. We can also pass the current sum in our recursive calls. However, then we'd also need to pass the required sum as an additional variable since we'd have to compare the current sum against that value. By passing in remaining sum, we can avoid having to pass additional variable and just see if the remaining sum is 0 (or equal to the value of the current node).
Finally, we'll have to pass a list of nodes here which will simply contain the list of all the nodes we have seen till now on the current branch. Let's call this pathNodes.
The following examples assume the sum to be found is 22.
At every step along the way, we will simply check if the remaining sum is equal to the value of the current node. If that is the case and the current node is a leaf node, we will add the current pathNodes to the final list of paths that we have to return as a result.
The problem statement here specifically mentions root to leaf paths. A slight modification is to find all root to node paths. The solutions are almost similar except that we'd get rid of the leaf check.
An important thing to consider for this modification is that the problem statement doesn't mention anything about the values of the nodes. That means, we can't assume them to be positive. Had the values been positive, we could stop at the node where the sum became equal to the node's value.
However, if the values of the nodes can be negative, then we have to traverse all the branches, all the way up to the roots. Let's look at a modified tree for reference.
We process one node at a time and every time the value of the remaining sum becomes equal to the value of the current node, we add the pathNodes to our final list. Let's go ahead and look at the implementation for this algorithm.

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    
    private void recurseTree(TreeNode node, int remainingSum, List<Integer> pathNodes, List<List<Integer>> pathsList) {
        
        if (node == null) {
            return;
        }
        
        // Add the current node to the path's list
        pathNodes.add(node.val);
        
        // Check if the current node is a leaf and also, if it
        // equals our remaining sum. If it does, we add the path to
        // our list of paths
        if (remainingSum == node.val && node.left == null && node.right == null) {
            pathsList.add(new ArrayList<>(pathNodes));
        } else {
            
            // Else, we will recurse on the left and the right children
            this.recurseTree(node.left, remainingSum - node.val, pathNodes, pathsList);
            this.recurseTree(node.right, remainingSum - node.val, pathNodes, pathsList);
        }
        
        // We need to pop the node once we are done processing ALL of it's
        // subtrees.
        pathNodes.remove(pathNodes.size() - 1);
    }
    
    public List<List<Integer>> pathSum(TreeNode root, int sum) {
        List<List<Integer>> pathsList = new ArrayList<List<Integer>>();
        List<Integer> pathNodes = new ArrayList<Integer>();
        this.recurseTree(root, sum, pathNodes, pathsList);
        return pathsList;        
    }
}

Complexity Analysis
Time Complexity: $O(N^2)$ where $N$ are the number of nodes in a tree. In the worst case, we could have a complete binary tree and if that is the case, then there would be $N/2$ leafs. For every leaf, we perform a potential $O(N)$ operation of copying over the pathNodes nodes to a new list to be added to the final pathsList. Hence, the complexity in the worst case could be $O(N^2)$.
Space Complexity: $O(N)$. The space complexity, like many other problems is debatable here. I personally choose not to consider the space occupied by the output in the space complexity. So, all the new lists that we create for the paths are actually a part of the output and hence, don't count towards the final space complexity. The only additional space that we use is the pathNodes list to keep track of nodes along a branch.
We could include the space occupied by the new lists (and hence the output) in the space complexity and in that case the space would be $O(N^2)$. There's a great answer on Stack Overflow about whether to consider input and output space in the space complexity or not. I prefer not to include them.

Number of Islands

Given an m x n 2D binary grid grid which represents a map of '1's (land) and '0's (water), return the number of islands.

An island is surrounded by water and is formed by connecting adjacent lands horizontally or vertically. You may assume all four edges of the grid are all surrounded by water.

 

Example 1:

Input: grid = [
  ["1","1","1","1","0"],
  ["1","1","0","1","0"],
  ["1","1","0","0","0"],
  ["0","0","0","0","0"]
]
Output: 1

Example 2:

Input: grid = [
  ["1","1","0","0","0"],
  ["1","1","0","0","0"],
  ["0","0","1","0","0"],
  ["0","0","0","1","1"]
]
Output: 3

Approach DFS [Accepted]
Intuition
Treat the 2d grid map as an undirected graph and there is an edge between two horizontally or vertically adjacent nodes of value '1'.
Algorithm
Linear scan the 2d grid map, if a node contains a '1', then it is a root node that triggers a Depth First Search. During DFS, every visited node should be set as '0' to mark as visited node. Count the number of root nodes that trigger DFS, this number would be the number of islands since each DFS starting at some root identifies an island.
class Solution {
  void dfs(char[][] grid, int r, int c) {
    int nr = grid.length;
    int nc = grid[0].length;
    if (r < 0 || c < 0 || r >= nr || c >= nc || grid[r][c] == '0') {
      return;
    }
    grid[r][c] = '0';
    dfs(grid, r - 1, c);
    dfs(grid, r + 1, c);
    dfs(grid, r, c - 1);
    dfs(grid, r, c + 1);
  }

  public int numIslands(char[][] grid) {
    if (grid == null || grid.length == 0) {
      return 0;
    }
    int nr = grid.length;
    int nc = grid[0].length;
    int num_islands = 0;
    for (int r = 0; r < nr; ++r) {
      for (int c = 0; c < nc; ++c) {
        if (grid[r][c] == '1') {
          ++num_islands;
          dfs(grid, r, c);
        }
      }
    }
    return num_islands;
  }
}

Interleaving String

Given strings s1, s2, and s3, find whether s3 is formed by an interleaving of s1 and s2.

An interleaving of two strings s and t is a configuration where they are divided into non-empty substrings such that:

• s = s1 + s2 + ... + sn
• t = t1 + t2 + ... + tm
• |n - m| <= 1
• The interleaving is s1 + t1 + s2 + t2 + s3 + t3 + ... or t1 + s1 + t2 + s2 + t3 + s3 + ...

Note: a + b is the concatenation of strings a and b.

 

Example 1:

Input: s1 = "aabcc", s2 = "dbbca", s3 = "aadbbcbcac"
Output: true

Example 2:

Input: s1 = "aabcc", s2 = "dbbca", s3 = "aadbbbaccc"
Output: false

Example 3:

Input: s1 = "", s2 = "", s3 = ""
Output: true

 

Constraints:

• 0 <= s1.length, s2.length <= 100
• 0 <= s3.length <= 200
• s1, s2, and s3 consist of lowercase English letters.

 

Approach 3: Using 2D Dynamic Programming

Algorithm

The recursive approach discussed in above solution included a character from one of the strings $s1$ or $s2$ in the resultant interleaved string and called a recursive function to check whether the remaining portions of $s1$ and $s2$ can be interleaved to form the remaining portion of $s3$. In the current approach, we look at the same problem the other way around. Here, we include one character from $s1$ or $s2$ and check whether the resultant string formed so far by one particular interleaving of the the current prefix of $s1$ and $s2$ form a prefix of $s3$.

Thus, this approach relies on the fact that the in order to determine whether a substring of $s3$(upto index $k$), can be formed by interleaving strings $s1$ and $s2$ upto indices $i$ and $j$ respectively, solely depends on the characters of $s1$ and $s2$ upto indices $i$ and $j$ only and not on the characters coming afterwards.

To implement this method, we'll make use of a 2D boolean array $dp$. In this array $dp[i][j]$ implies if it is possible to obtain a substring of length $(i+j+2)$ which is a prefix of $s3$ by some interleaving of prefixes of strings $s1$ and $s2$ having lengths $(i+1)$ and $(j+1)$ respectively. For filling in the entry of $dp[i][j]$, we need to consider two cases:

1. The character just included i.e. either at $i^{th}$ index of $s1$ or at $j^{th}$ index of $s2$ doesn't match the character at $k^{th}$ index of $s3$, where $k=i+j+1$. In this case, the resultant string formed using some interleaving of prefixes of $s1$ and $s2$ can never result in a prefix of length $k+1$ in $s3$. Thus, we enter $False$ at the character $dp[i][j]$.

2. The character just included i.e. either at $i^{th}$ index of $s1$ or at $j^{th}$ index of $s2$ matches the character at $k^{th}$ index of $s3$, where $k=i+j+1$. Now, if the character just included(say $x$) which matches the character at $k^{th}$ index of $s3$, is the character at $i^{th}$ index of $s1$, we need to keep $x$ at the last position in the resultant interleaved string formed so far. Thus, in order to use string $s1$ and $s2$ upto indices $i$ and $j$ to form a resultant string of length $(i+j+2)$ which is a prefix of $s3$, we need to ensure that the strings $s1$ and $s2$ upto indices $(i-1)$ and $j$ respectively obey the same property.

Similarly, if we just included the $j^{th}$ character of $s2$, which matches with the $k^{th}$ character of $s3$, we need to ensure that the strings $s1$ and $s2$ upto indices $i$ and $(j-1)$ also obey the same property to enter a $true$ at $dp[i][j]$.

This can be made clear with the following example:

s1="aabcc"
s2="dbbca"
s3="aadbbcbcac"

public class Solution {
    public boolean isInterleave(String s1, String s2, String s3) {
        if (s3.length() != s1.length() + s2.length()) {
            return false;
        }
        boolean dp[][] = new boolean[s1.length() + 1][s2.length() + 1];
        for (int i = 0; i <= s1.length(); i++) {
            for (int j = 0; j <= s2.length(); j++) {
                if (i == 0 && j == 0) {
                    dp[i][j] = true;
                } else if (i == 0) {
                    dp[i][j] = dp[i][j - 1] && s2.charAt(j - 1) == s3.charAt(i + j - 1);
                } else if (j == 0) {
                    dp[i][j] = dp[i - 1][j] && s1.charAt(i - 1) == s3.charAt(i + j - 1);
                } else {
                    dp[i][j] = (dp[i - 1][j] && s1.charAt(i - 1) == s3.charAt(i + j - 1))

                        || (dp[i][j - 1] && s2.charAt(j - 1) == s3.charAt(i + j - 1));
                }
            }
        }
        return dp[s1.length()][s2.length()];
    }
}    

Complexity Analysis
Time complexity : $O(m \cdot n)$. dp array of size $m*n$ is filled.
Space complexity : $O(m \cdot n)$. 2D dp of size $(m+1)*(n+1)$ is required. $m$ and $n$ are the lengths of strings $s1$ and $s2$ respectively.