Path Sum II

Given the root of a binary tree and an integer targetSum, return all root-to-leaf paths where each path's sum equals targetSum.

A leaf is a node with no children.

 

Example 1:

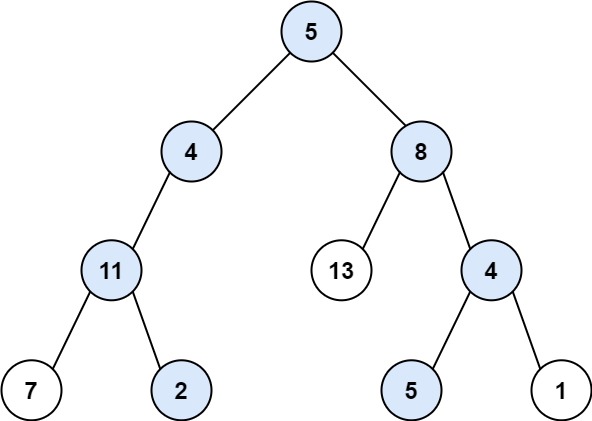
Input: root = [5,4,8,11,null,13,4,7,2,null,null,5,1], targetSum = 22
Output: [[5,4,11,2],[5,8,4,5]]

Example 2:

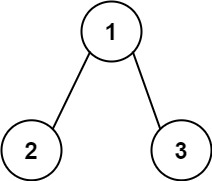
Input: root = [1,2,3], targetSum = 5
Output: []

Example 3:

Input: root = [1,2], targetSum = 0
Output: []

Solution
Approach: Depth First Traversal | Recursion
Intuition
The intuition for this approach is pretty straightforward. The problem statement asks us to find all root to leaf paths in a given binary tree. If you simply consider the depth first traversal on a tree, all it does is traverse once branch after another. All we need to do here is to simply execute the depth first traversal and maintain two things along the way:
A running sum of all the nodes traversed till that point in recursion and
A list of all those nodes
If ever the sum becomes equal to the required sum, and the node where this happens is a leaf node, we can simply add the list of nodes to our final solution. We keep on doing this for every branch of the tree and we will get all the root to leaf paths in this manner that add up to a certain value. Basically, these paths are branches and hence the depth first traversal makes the most sense here. We can also use the breadth first approach for solving this problem. However, that would be super heavy on memory and is not a recommended approach for this very problem. We will look into more details towards the end.
Algorithm
We'll define a function called recurseTree which will take the following parameters
node which represents the current node we are on during recursion
remainingSum which represents the remaining sum that we need to find going down the tree. We can also pass the current sum in our recursive calls. However, then we'd also need to pass the required sum as an additional variable since we'd have to compare the current sum against that value. By passing in remaining sum, we can avoid having to pass additional variable and just see if the remaining sum is 0 (or equal to the value of the current node).
Finally, we'll have to pass a list of nodes here which will simply contain the list of all the nodes we have seen till now on the current branch. Let's call this pathNodes.
The following examples assume the sum to be found is 22.
At every step along the way, we will simply check if the remaining sum is equal to the value of the current node. If that is the case and the current node is a leaf node, we will add the current pathNodes to the final list of paths that we have to return as a result.
The problem statement here specifically mentions root to leaf paths. A slight modification is to find all root to node paths. The solutions are almost similar except that we'd get rid of the leaf check.
An important thing to consider for this modification is that the problem statement doesn't mention anything about the values of the nodes. That means, we can't assume them to be positive. Had the values been positive, we could stop at the node where the sum became equal to the node's value.
However, if the values of the nodes can be negative, then we have to traverse all the branches, all the way up to the roots. Let's look at a modified tree for reference.
We process one node at a time and every time the value of the remaining sum becomes equal to the value of the current node, we add the pathNodes to our final list. Let's go ahead and look at the implementation for this algorithm.

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    
    private void recurseTree(TreeNode node, int remainingSum, List<Integer> pathNodes, List<List<Integer>> pathsList) {
        
        if (node == null) {
            return;
        }
        
        // Add the current node to the path's list
        pathNodes.add(node.val);
        
        // Check if the current node is a leaf and also, if it
        // equals our remaining sum. If it does, we add the path to
        // our list of paths
        if (remainingSum == node.val && node.left == null && node.right == null) {
            pathsList.add(new ArrayList<>(pathNodes));
        } else {
            
            // Else, we will recurse on the left and the right children
            this.recurseTree(node.left, remainingSum - node.val, pathNodes, pathsList);
            this.recurseTree(node.right, remainingSum - node.val, pathNodes, pathsList);
        }
        
        // We need to pop the node once we are done processing ALL of it's
        // subtrees.
        pathNodes.remove(pathNodes.size() - 1);
    }
    
    public List<List<Integer>> pathSum(TreeNode root, int sum) {
        List<List<Integer>> pathsList = new ArrayList<List<Integer>>();
        List<Integer> pathNodes = new ArrayList<Integer>();
        this.recurseTree(root, sum, pathNodes, pathsList);
        return pathsList;        
    }
}

Complexity Analysis
Time Complexity: $O(N^2)$ where $N$ are the number of nodes in a tree. In the worst case, we could have a complete binary tree and if that is the case, then there would be $N/2$ leafs. For every leaf, we perform a potential $O(N)$ operation of copying over the pathNodes nodes to a new list to be added to the final pathsList. Hence, the complexity in the worst case could be $O(N^2)$.
Space Complexity: $O(N)$. The space complexity, like many other problems is debatable here. I personally choose not to consider the space occupied by the output in the space complexity. So, all the new lists that we create for the paths are actually a part of the output and hence, don't count towards the final space complexity. The only additional space that we use is the pathNodes list to keep track of nodes along a branch.
We could include the space occupied by the new lists (and hence the output) in the space complexity and in that case the space would be $O(N^2)$. There's a great answer on Stack Overflow about whether to consider input and output space in the space complexity or not. I prefer not to include them.

Word Ladder

 A transformation sequence from word beginWord to word endWord using a dictionary wordList is a sequence of words beginWord -> s1 -> s2 -> ... -> sk such that:

• Every adjacent pair of words differs by a single letter.
• Every si for 1 <= i <= k is in wordList. Note that beginWord does not need to be in wordList.
• sk == endWord

Given two words, beginWord and endWord, and a dictionary wordList, return the number of words in the shortest transformation sequence from beginWord to endWord, or 0 if no such sequence exists.

 

Example 1:

Input: beginWord = "hit", endWord = "cog", wordList = ["hot","dot","dog","lot","log","cog"]
Output: 5
Explanation: One shortest transformation sequence is "hit" -> "hot" -> "dot" -> "dog" -> cog", which is 5 words long.

Example 2:

Input: beginWord = "hit", endWord = "cog", wordList = ["hot","dot","dog","lot","log"]
Output: 0
Explanation: The endWord "cog" is not in wordList, therefore there is no valid transformation sequence.

 

Constraints:

• 1 <= beginWord.length <= 10
• endWord.length == beginWord.length
• 1 <= wordList.length <= 5000
• wordList[i].length == beginWord.length
• beginWord, endWord, and wordList[i] consist of lowercase English letters.
• beginWord != endWord
• All the words in wordList are unique.

Solution Article

We are given a beginWord and an endWord. Let these two represent start node and end node of a graph. We have to reach from the start node to the end node using some intermediate nodes/words. The intermediate nodes are determined by the wordList given to us. The only condition for every step we take on this ladder of words is the current word should change by just one letter.

We will essentially be working with an undirected and unweighted graph with words as nodes and edges between words which differ by just one letter. The problem boils down to finding the shortest path from a start node to a destination node, if there exists one. Hence it can be solved using Breadth First Search approach.

One of the most important step here is to figure out how to find adjacent nodes i.e. words which differ by one letter. To efficiently find the neighboring nodes for any given word we do some pre-processing on the words of the given wordList. The pre-processing involves replacing the letter of a word by a non-alphabet say, *.

This pre-processing helps to form generic states to represent a single letter change.

For e.g. Dog ----> D*g <---- Dig

Both Dog and Dig map to the same intermediate or generic state D*g.

The preprocessing step helps us find out the generic one letter away nodes for any word of the word list and hence making it easier and quicker to get the adjacent nodes. Otherwise, for every word we will have to iterate over the entire word list and find words that differ by one letter. That would take a lot of time. This preprocessing step essentially builds the adjacency list first before beginning the breadth first search algorithm.

For eg. While doing BFS if we have to find the adjacent nodes for Dug we can first find all the generic states for Dug.

1. Dug => *ug
2. Dug => D*g
3. Dug => Du*

The second transformation D*g could then be mapped to Dog or Dig, since all of them share the same generic state. Having a common generic transformation means two words are connected and differ by one letter.

Approach : Breadth First Search

Intuition

Start from beginWord and search the endWord using BFS.

Algorithm

1. Do the pre-processing on the given wordList and find all the possible generic/intermediate states. Save these intermediate states in a dictionary with key as the intermediate word and value as the list of words which have the same intermediate word.

2. Push a tuple containing the beginWord and 1 in a queue. The 1 represents the level number of a node. We have to return the level of the endNode as that would represent the shortest sequence/distance from the beginWord.

3. To prevent cycles, use a visited dictionary.

4. While the queue has elements, get the front element of the queue. Let's call this word as current_word.

5. Find all the generic transformations of the current_word and find out if any of these transformations is also a transformation of other words in the word list. This is achieved by checking the all_combo_dict.

6. The list of words we get from all_combo_dict are all the words which have a common intermediate state with the current_word. These new set of words will be the adjacent nodes/words to current_word and hence added to the queue.

7. Hence, for each word in this list of intermediate words, append (word, level + 1) into the queue where level is the level for the current_word.

8. Eventually if you reach the desired word, its level would represent the shortest transformation sequence length.

   Termination condition for standard BFS is finding the end word.

   class Solution {

     public int ladderLength(String beginWord, String endWord, List<String> wordList) {

       // Since all words are of same length.

       int L = beginWord.length();

       // Dictionary to hold combination of words that can be formed,

       // from any given word. By changing one letter at a time.

       Map<String, List<String>> allComboDict = new HashMap<>();

       wordList.forEach(

           word -> {

             for (int i = 0; i < L; i++) {

               // Key is the generic word

               // Value is a list of words which have the same intermediate generic word.

               String newWord = word.substring(0, i) + '*' + word.substring(i + 1, L);

               List<String> transformations = allComboDict.getOrDefault(newWord, new ArrayList<>());

               transformations.add(word);

               allComboDict.put(newWord, transformations);

             }

           });

       // Queue for BFS

       Queue<Pair<String, Integer>> Q = new LinkedList<>();

       Q.add(new Pair(beginWord, 1));

       // Visited to make sure we don't repeat processing same word.

       Map<String, Boolean> visited = new HashMap<>();

       visited.put(beginWord, true);

       while (!Q.isEmpty()) {

         Pair<String, Integer> node = Q.remove();

         String word = node.getKey();

         int level = node.getValue();

         for (int i = 0; i < L; i++) {

           // Intermediate words for current word

           String newWord = word.substring(0, i) + '*' + word.substring(i + 1, L);

           // Next states are all the words which share the same intermediate state.

           for (String adjacentWord : allComboDict.getOrDefault(newWord, new ArrayList<>())) {

             // If at any point if we find what we are looking for

             // i.e. the end word - we can return with the answer.

             if (adjacentWord.equals(endWord)) {

               return level + 1;

             }

             // Otherwise, add it to the BFS Queue. Also mark it visited

             if (!visited.containsKey(adjacentWord)) {

               visited.put(adjacentWord, true);

               Q.add(new Pair(adjacentWord, level + 1));

             }

           }

         }

       }

       return 0;

     }

   } 

Complexity Analysis

• Time Complexity: $O({M}^2 \times N)$, where $M$ is the length of each word and $N$ is the total number of words in the input word list.

  • For each word in the word list, we iterate over its length to find all the intermediate words corresponding to it. Since the length of each word is $M$ and we have $N$ words, the total number of iterations the algorithm takes to create all_combo_dict is $M \times N$. Additionally, forming each of the intermediate word takes $O(M)$ time because of the substring operation used to create the new string. This adds up to a complexity of $O({M}^2 \times N)$.

  • Breadth first search in the worst case might go to each of the $N$ words. For each word, we need to examine $M$ possible intermediate words/combinations. Notice, we have used the substring operation to find each of the combination. Thus, $M$ combinations take $O({M} ^ 2)$ time. As a result, the time complexity of BFS traversal would also be $O({M}^2 \times N)$.

  Combining the above steps, the overall time complexity of this approach is $O({M}^2 \times N)$.

• Space Complexity: $O({M}^2 \times N)$.

  • Each word in the word list would have $M$ intermediate combinations. To create the all_combo_dict dictionary we save an intermediate word as the key and its corresponding original words as the value. Note, for each of $M$ intermediate words we save the original word of length $M$. This simply means, for every word we would need a space of ${M}^2$ to save all the transformations corresponding to it. Thus, all_combo_dict would need a total space of $O({M}^2 \times N)$.
  • Visited dictionary would need a space of $O(M \times N)$ as each word is of length $M$.
  • Queue for BFS in worst case would need a space for all $O(N)$ words and this would also result in a space complexity of $O(M \times N)$.

  Combining the above steps, the overall space complexity is $O({M}^2 \times N)$ + $O(M * N)$ + $O(M * N)$ = $O({M}^2 \times N)$ space.

Optimization: We can definitely reduce the space complexity of this algorithm by storing the indices corresponding to each word instead of storing the word itself.